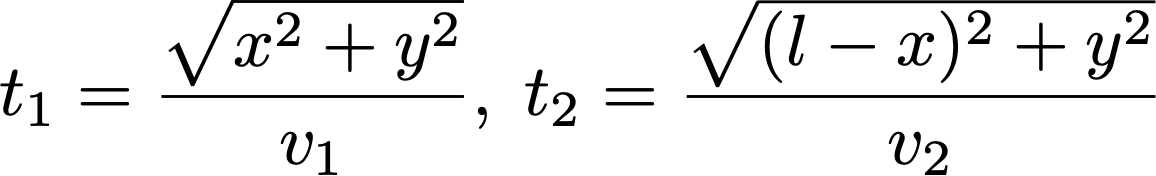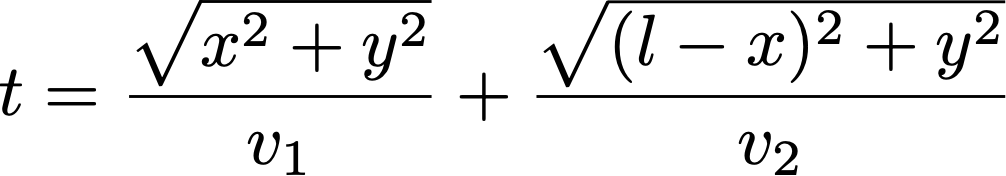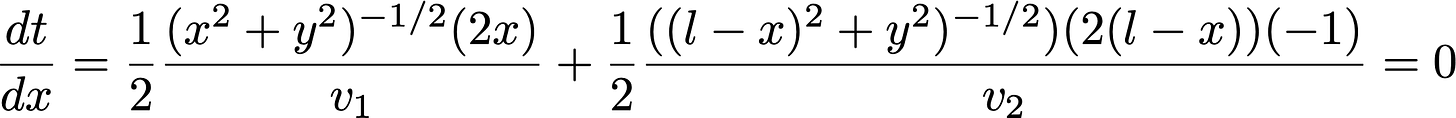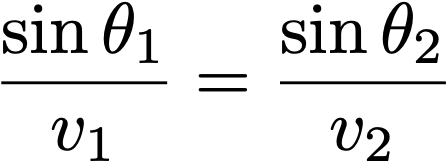So there’s a dog. She sees a ball and wants the ball, but the ball is floating in a swimming pool. And the dog must get the ball as soon as possible, naturally. This is a classic pattern in physics — how to choose a path to minimize some quantity (here, the time taken to travel along the path). So what should she do? Make a diagram!
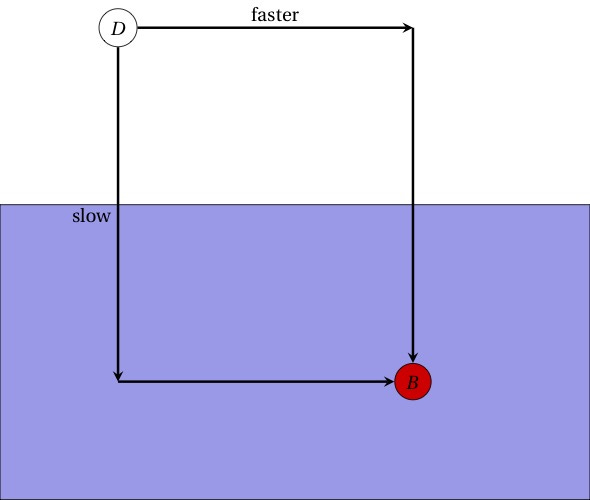
Ok, so the dog wants to follow the path that will minimize the overall time from her position (D) to the ball in the pool (B). Thinking about it for a minute, she realizes that some paths are clearly better than others. For example, running straight into the water immediately and then swimming over to the ball isn’t too smart; since she runs way faster than she can swim, she would be spending a lot of time going slowly. The path labeled “faster” is a better idea since she’s spending lots of time going fast and the minimum amount of time going slowly.
But maybe that “faster” path bothers you a bit — it’s certainly faster than the “slow” path, but maybe she can improve on it a little. In terms of distance, it’s a pretty long path, so maybe something more diagonal (and direct) would reduce the overall time because the path is shorter (even though there would be a little more time spent going slowly). Maybe the real answer is just to take the true diagonal path directly towards the ball!
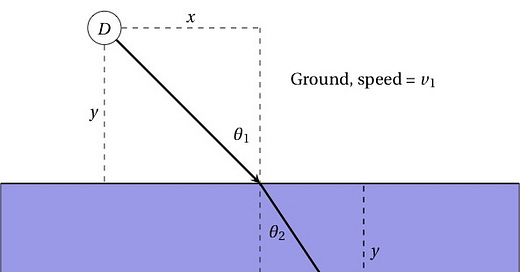
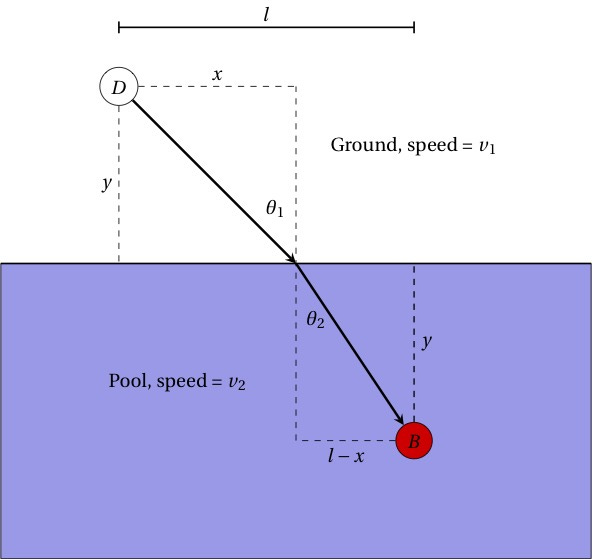
What she really wants to know is the entry point (we’ll call it x) where she needs to enter the water, some horizontal distance away from where she starts at D. If the horizontal distance to the ball is l, then the true diagonal path would be when x is half of l. To make things simpler to calculate for her, suppose the distance away from the ground/water line is the same for D and B (call it y). Then we’d have this:
What are we minimizing? The time. So let’s write down the time taken (just diagonal distance traveled divided by speed) along the ground as well as in the pool:
The total time t, then, is just those two added together:
Now what the dog remembers from Calculus 1 is that, to minimize a function, she needs to take the derivative of the function and set it equal to zero. Derivative with respect to what? x! In words, remember that the derivative is telling you how the time changes as we vary x (the entry point). And if this time is a minimum, the change of the function will be zero if we vary x a little bit. The derivative takes a little bit of work since our variable x is buried inside a couple of functions. Chain rule! That’s fine, though, since the dog is obviously a working breed, so she’ll enjoy a bit of hard work:
which then simplifies a bit to
Admittedly, finding the right entry point is a bit difficult for her to calculate from this, but then she might notice that the left side of the equation is just the sine of the entry angle (relative to the normal to the ground/water line), and the right side is similar:
So the final path with the minimal time will look like this relationship between the angles involved and the speeds. Notice that if the speeds are the same, the angles are then the same too, which would be a straight diagonal path. If the running speed is more than the swimming speed, then you can see that the top angle has to be greater than the bottom angle. The astonishing thing is that this is exactly the same equation used to calculate the deflection of a light beam as it travels from one medium to another — the phenomenon of refraction (in this case, the above equation is called Snell’s Law).
What I love about this is the hidden beauty inside some dry-looking equations. Physics students see the above formula and use it to calculate angles of refraction, perhaps without much drama. Put in a set of numbers you know, calculate another number. But what gets physicists hearts beating faster is the underlying principle behind both scenarios — it’s not at all obvious that Snell’s Law is describing a minimal principle. Finding out that seemingly different phenomena are actually unified and predicted by a simple principle is what the pursuit of physics is all about, really.
Fermat’s Principle
The French mathematician Pierre de Fermat (in 1662!) applied this kind of analysis to the problem of describing a beam of light as it passes from, say, air into a more dense medium:
His idea was that the light path will be the one that takes the minimum time between two points. Why does this result in a “bent” path? Because light travels more slowly in the dense medium than in the air! The idea that Nature optimizes some path to minimize a quantity is an extremely deep and powerful one that is found all throughout physics — no doubt we’ll explore this in future articles…
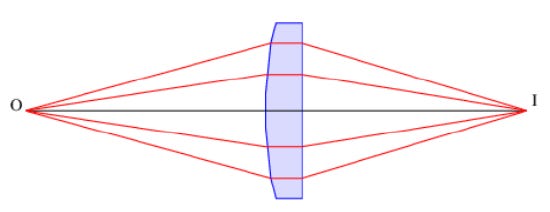
A cool example of how this works is the property of a convex lens to focus light to a point. Imagine the source O emitting light beams in all directions — one particular beam goes straight through the middle of a lens (the thickest part!) to a point I. Look at a beam almost in the same direction — it hits the lens and is refracted to the point I also. Check out that path! It’s a little longer (in distance) than the “straight” path. But since the lens is curved, there’s a little less lens to travel through, so the overall path takes the same amount of time. The same idea applies to the next beam up — longer distance, but less lens to pass through, so the time is equal. So a really interesting way to think about a lens is that it’s a device to sort of “fool” Nature into making lots of beams take the same amount of time to reach a point. If two paths take the same amount of time, how does light decide which one to take? It takes all of them! The result is what we call a “focused” beam. [For lots more, refer to the ever-amazing resource The Feynman Lectures on Physics, Vol. 1, Chapter 26]
On Deck:
The next article I’m working on is how we found out (and really know) the incredible distances to the planets and stars!
If you’re a student/teacher and want to see lots of worked examples that I like to include in my classes when I teach the “standard” University Physics 1 and 2 courses, feel free to browse the (growing) collection of 150+ videos at
And if something is especially cool and you’re inclined to leave a “tip” I’m not above coffee or pizza:
Thanks for reading First Excited State! Subscribe for free to receive new posts automatically!