Global Warming -- A Toy Greenhouse Effect Model Using First-Year Physics
Public “debates” over global warming and climate change are often not substantive exchanges since only rarely do all the parties involved have any kind of expertise in the subject. For a topic with such profound implications regarding public policy and our future, though, I think we can get a pretty good understanding of the basic principles with just a bit of physics and mathematics at our backs.
It's fun to build "toy" models of how things should work just to see if a known effect can be modeled and understood, even approximately. Here, I'll try to trace some fairly simple calculations, all of which have certainly been done better elsewhere, just as an exercise to try to understand the order-of-magnitude effect of “heat-trapping” by an IR-absorbing gas like carbon dioxide.
Temperature and Energy Balance
The idea is to appeal to the basic physics of energy conservation. Whatever energy the Earth gets from the Sun must be re-radiated out into space for the temperature to be in some sort of equilibrium. The first step, then, is to calculate how much energy we intercept from the Sun each second. Well, really, I suppose the zeroth step is to calculate how much energy the Sun actually emits each second.

Looking at the spectrum of the Sun, it glows as an approximate blackbody (a perfect absorber and thermal radiator) with an effective "surface" temperature of about 5780 K. The amount of energy generated per second (the luminosity) by a glowing object is given by the Stefan-Boltzmann Law, and depends on two things: its temperature and size:
Then we imagine that this total energy, emitted uniformly in all directions, is spread out around the inside of a gigantic sphere extending all the way out to the Earth's distance from the Sun. Since the imaginary sphere completely wraps around the Sun, we know that it absorbs all the Sun's energy; in particular, each square meter of the surface absorbs only a tiny fraction of the total luminosity --- we just divide by the total surface area of the sphere to get the solar flux through each square meter:
where is the radius of this big sphere. So, in principle, each square meter directly facing the Sun receives this much energy per second. The problem is that not every square meter on the surface of the Earth points at the Sun --- close to the equator this is a pretty good approximation, but at the poles the sunlight is much more indirect.

You might recognize that the right way to calculate the flux would be to integrate the amount of flux across the hemisphere that faces the Sun, but that sounds hard, and it contradicts a fundamental principle of astrophysics: laziness. Stopping to think for a minute, what we want is the amount of solar radiation intercepted by the Earth — but if we imagine a (large) screen behind the Earth, the intercepted radiation is just the shadow cast. Or, in other words, just the circular cross section! So then the total solar energy per second received by Earth is
Actually, this is still not quite right. Not all the solar energy falling on the Earth is absorbed; some of it is reflected back into space by the surface, atmosphere, and clouds. The percentage reflected back is called the albedo, and for the Earth an average value is about 0.30. So that means that only about 70% of the solar radiation reaches the surface and warms the planet. The expression, then, for the solar radiation warming the Earth (in Watts) is
Finally, let's invoke the physics of energy balance --- if the Earth receives that much energy, and it's in equilibrium, it must radiate that much energy as well. A subtle point, though, is that Earth radiates this energy over its entire spherical surface area. So now we just make the Earth a radiator just as we did for the Sun to begin with, and set incoming radiation equal to outgoing:
Now we can solve for the “effective” (radiative) temperature of the Earth!
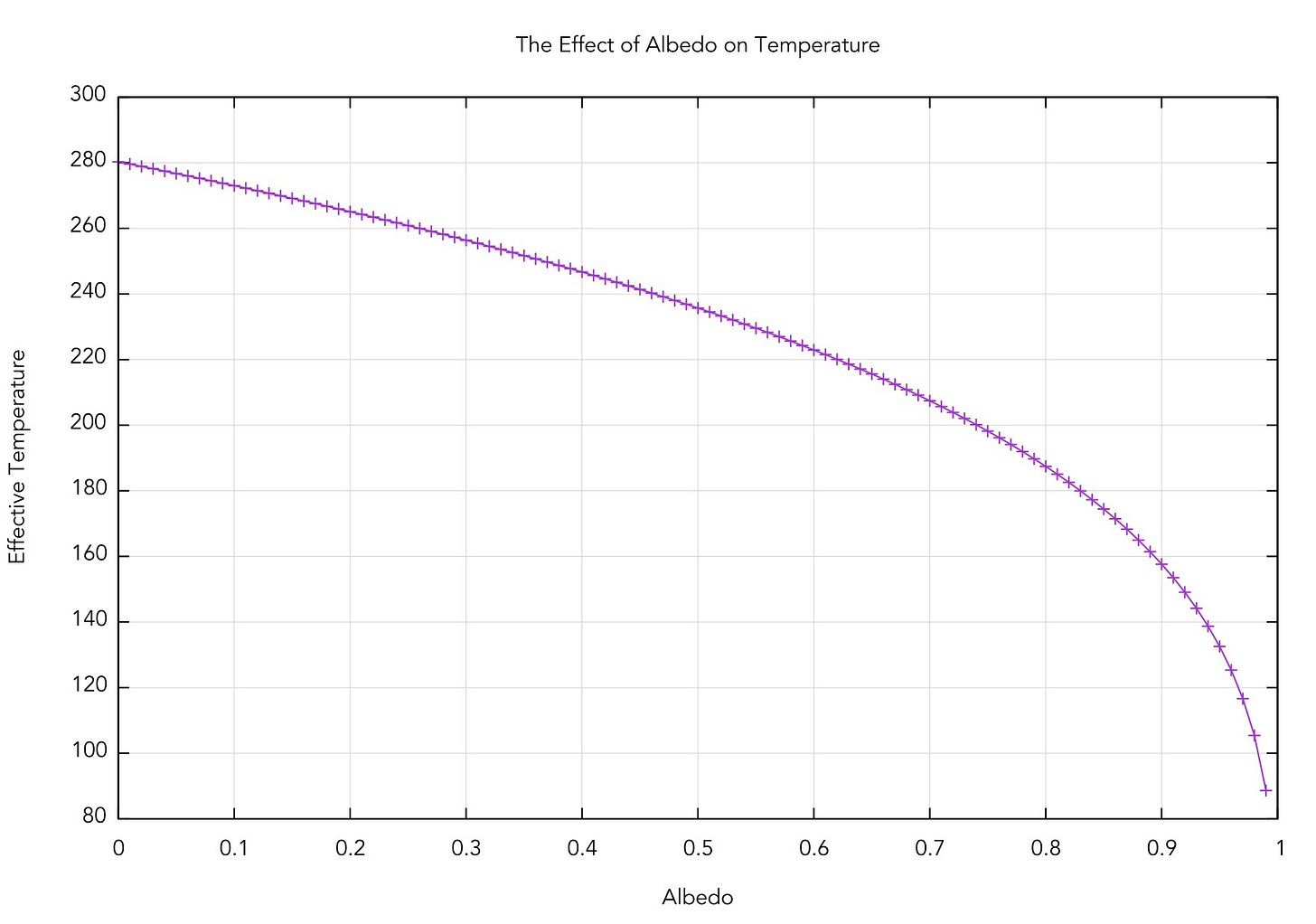
after plugging in the numbers. The effective temperature is sensitive to high albedo, as you can see in the plot below. A perfectly absorbing (black) Earth would have a temperature of 280 K; however, a highly reflective Earth (perhaps covered in snow/ice, having an albedo of about 0.85) would be far cooler. That most likely had significant effects in the past.
Since 273 K is the point where water freezes, an average temperature of 256 K is a little strange --- it's hard to imagine much liquid water on the surface if that’s the average! The Earth really has an average effective temperature of 288 K, so we’ve missed something. So far, all we've really done is calculate the temperature of a bare rock without accounting for the effect of an atmosphere.
How well does this simple model do? There are some examples of “bare rocks” in the Solar System, or at least objects with thin atmospheres, so let’s check their predicted vs. real temperatures (just adjust the solar flux above at their location and use the above equation with their albedos!):
Pretty good! So now let’s see what effect a “Greenhouse” atmosphere can make:
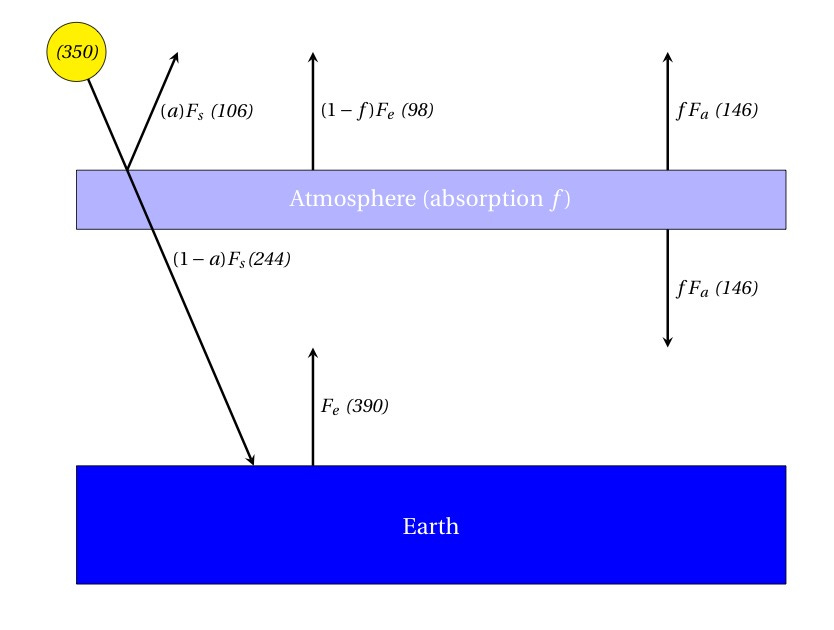
One simple way to model an absorbing atmosphere is to imagine a single layer that is transparent to the Sun's visible radiation, but absorbs infrared radiation (heat) emitted from the ground.
Radiation from the Sun (350 Watts per square meter averaged over Earth’s entire surface) encounters the atmosphere and some fraction of it warms the ground; the remainder is the albedo which is reflected back into space. If this is all that happens, then we’re back to the “bare rock” idea above — the effective temperature of that flux is
The new idea: let’s say our model atmosphere absorbs some fraction f of the radiation given off by the warmed Earth. But, crucially, this energy doesn’t disappear — the atmosphere then has to radiate it back in all directions, so some of it returns to further warm the surface. This is the “Greenhouse Effect”! So what we do is set up energy balance equations for the 3 regions: space, atmosphere, and surface (here, written in terms of fluxes averaged over the whole surface):
Almost done! Now solve for Fe (the energy flux radiated by Earth’s surface) and calculate the temperature:
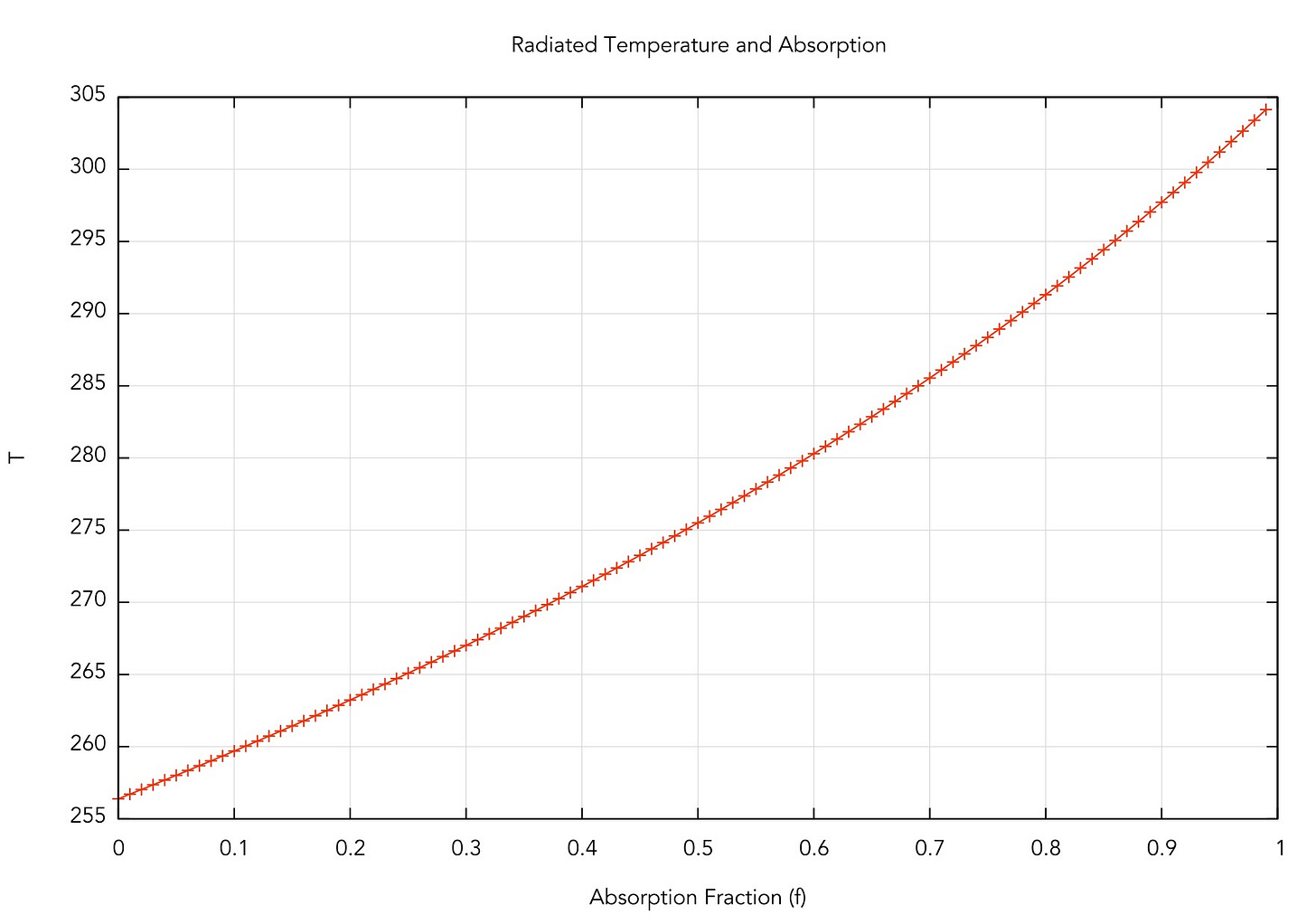
Let’s plot this as a function of f:
This makes total sense! If there’s no absorption, we're back to the "bare rock" we had before (256 K), but interestingly, if f = 1 (totally absorbing), we get a temperature of about 303 K. The observed global mean temp is about 288 K, meaning that the atmosphere absorbs about 75% of the infrared radiation emitted by the Earth (according to our very simple model and rounding off some numbers). Another cool thing is that we can calculate Ta, the temperature of the upper atmosphere, and it’s about 240 K for the simple model. This is interesting, and a smoking gun of the Greenhouse Effect: since the amount of energy from the Sun is constant, then if the lower atmosphere is heating, the upper atmosphere should be cooling to compensate.
One more thing — if one layer is perfectly absorbing, is there any effect of adding another layer on top of that one? Yes! That second layer will absorb and re-radiate energy too, raising the temperature of what’s underneath (just like layering blankets). You can carry out the same calculations with another equation for the new absorbing layer, and you’ll find the surface is now something like 335 K.
Moral: Lots of absorbing material = Oven Time!
Professionally detailed models include a dazzling number of effects and conditions, but what’s impressive is how far we can get with just a little bit of physics and math!
On Deck:
The next article I’m working on is an explanation of the “gravitational slingshot” maneuver we use to speed up spacecraft bound for the outer solar system.
If you’re a student/teacher and want to see lots of worked examples that I like to include in my classes when I teach the “standard” University Physics 1 and 2 courses, feel free to browse the (growing) collection of 150+ videos at
And if something is especially cool and you’re inclined to leave a “tip” I’m not above coffee or pizza: