Photos of the night sky often validate the ancient idea that the stars are tiny points of light stuck on a vast enveloping dome. While they vary in brightness, to be sure, we get no information about the depth of the Universe from simple observations of them. Even through most reasonable telescopes, stars all resolve to tiny sparks of light — it’s only recently with giant instruments that we can see the actual disks of stars.
So how can we find the distance to a point of light? The most direct way is to actually measure it using the classic technique of parallax (looking at the same object from 2 different places and working out the resulting sight-line triangles).
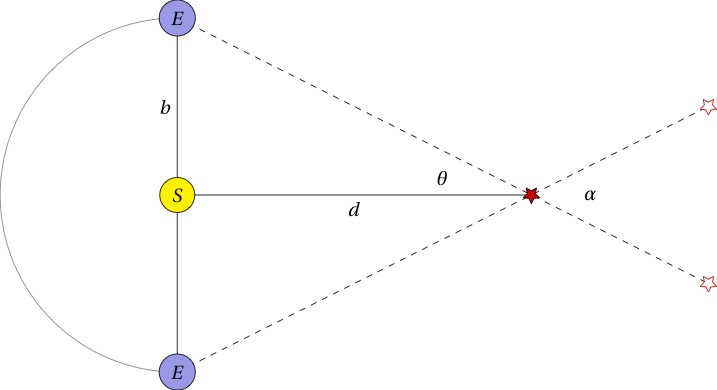
This is no different than putting your finger in front of your face and looking at it with one eye, and then switching eyes! The apparent position of your finger will change with respect to the background. And the key point is that the farther away your finger is, the smaller the “jump” in apparent position. We use the Earth’s position 6 months apart as each “eye”, and the star as our “finger”. To use our trigonometry, the parallax angle 𝜃 is usually half of the total angular shift in position observed (𝛼 in the diagram), so then there’s just a right triangle:
All we have to know is that baseline distance (b) and we’re all set.
Historical footnote: this is not a modern idea. Back in the geocentric days, they knew perfectly well that if we circled the Sun, we ought to see the positions of the stars shift during the year. This was never observed (no telescopes!), and actually used as evidence that we didn’t orbit the Sun!
As a local example, we can use this to (roughly) estimate the distance to the Moon. I used the excellent (free!) software Stellarium to simulate images of the Moon taken from two different places on the Earth at the same time. One is from 50 N latitude and one from 20 N latitude.
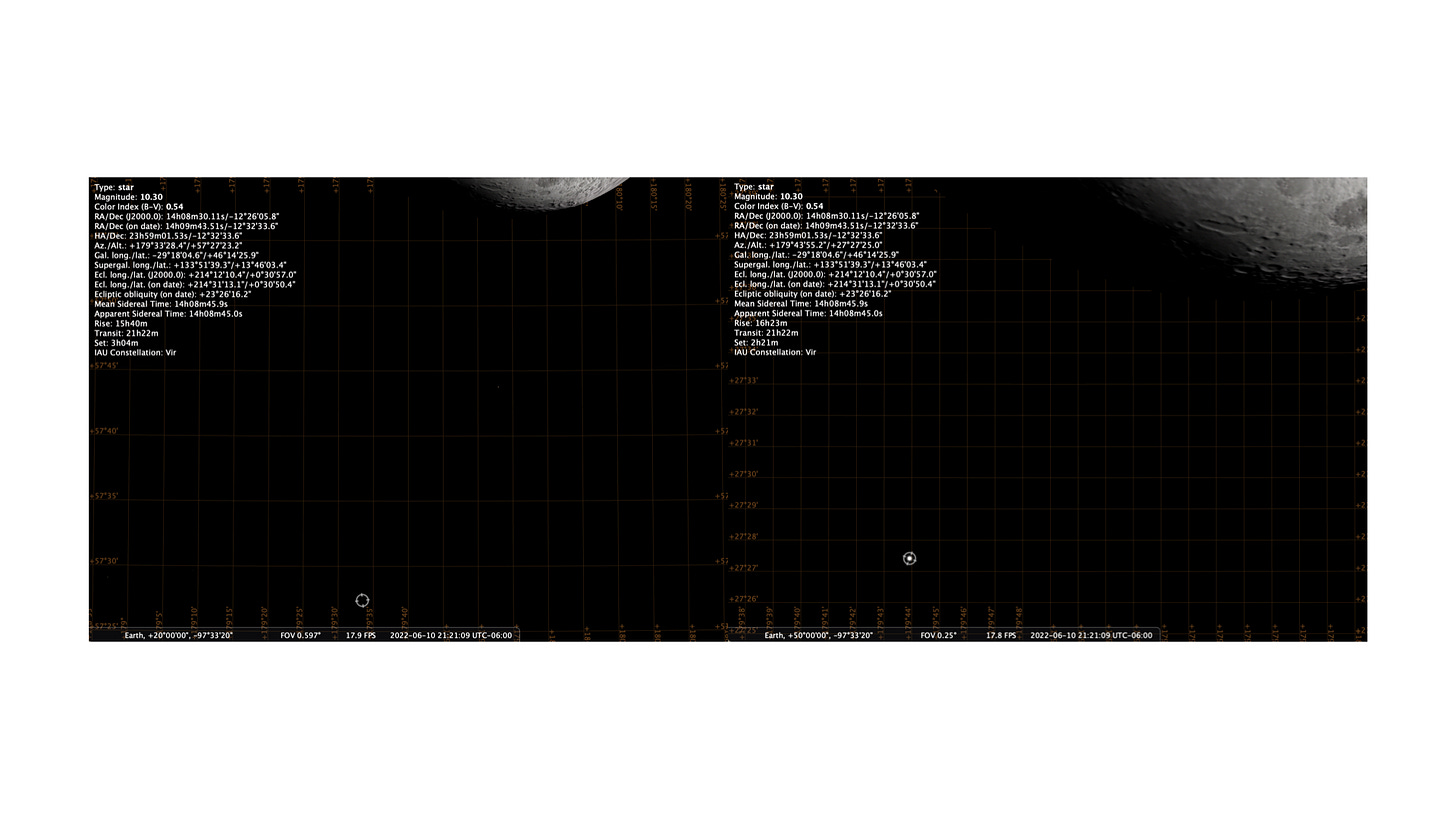
Just doing a very rough estimate, the angular shift of the Moon is about 23’ (23/60 of a degree) with respect to that background star. The baseline here is half the distance between 20 N and 50 N latitude, or about 1/12 of the full 40,000-km circumference of the Earth (3,333 km), without worrying much about the curved surface. Ok, so
This is something like 20% off from the “real” distance, but I was playing pretty fast and loose with the estimations (the moon isn’t directly overhead so it’s not exactly a right triangle, my baseline is too big because it’s along a curved surface, sloppy reading of the angle from the image, and so on).
The point is that this is a pretty straightforward way to calculate distances to objects close enough to exhibit a parallax shift. Once telescopes were good enough to finally see parallax shifts in nearby stars, we could start reliably mapping our local stellar neighborhood. The closest “star” to us, for example, is actually the triple star system Alpha Centauri, and its parallax angle is about 1” (1 arc-second, or 1/3600 degree). The human eye can make out details down to about 1’ ( 1/60 degree), so it’s no wonder this was never observed until the 1800s! Plugging in numbers, a star with a 1” parallax is at a distance of (in Astronomical Units, where 1 AU is the Earth-Sun distance)
This distance represented by a parallax shift of 1 arc-second is defined as a parsec (“parallax-second”, abbreviated “pc”) — about 200,000 times the Earth-Sun distance. Proxima actually has a shift of about 0.75”, so it’s roughly 1.3 parsecs away (each parsec is 3.26 light-years).
It’s easier to see the shift if the baseline is bigger, of course — check this out: here’s the shift of Proxima Centauri (the closest of the triple system right now) as seen from the Earth and the New Horizons probe in the outer solar system:

This method is limited by distance; stars that are too far away just don’t shift enough for us to measure. The Hipparchos orbiting telescope mission was dedicated to measuring parallax for the closest 100,000 stars (out to about 500 parsecs or so). Its successor is the Gaia mission, a remarkably sensitive probe that measured the distances of the closest billion stars (out to 2000 pc, less accurate measurements out to 10,000 pc).
Wow.
Farther!
Even the Gaia mission only lets us map a small section of our 30,000 pc Galaxy. To take the next step it turns out there are 3 stellar variables at play:
The amount of energy a star produces each second, called the Luminosity, measured in Watts. This is an intrinsic (or absolute) brightness, exactly like the rating of light bulbs. A 100-Watt bulb produces 100 Joules of energy every second no matter how far away it is from you.
The apparent brightness of a star — how bright the star actually looks to us here on Earth.
The distance to the star.
If you know two of these, you can calculate the other one since apparent brightness will decrease as the square of the distance. If you note the brightness of a 100-Watt bulb that is 1 meter away, you’ll find that if you move it 2 meters away it’ll be 1/4 as bright. 3 meters away, it’ll be 1/9 as bright, and so on.
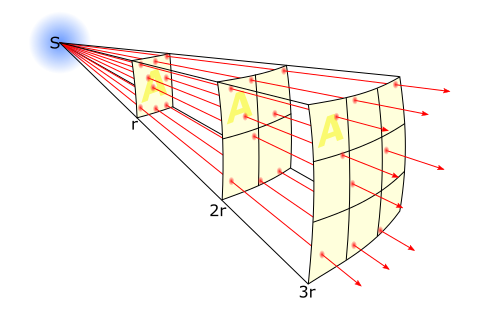
But here’s the problem: When we look at the stars, we can certainly measure how bright they appear to us, that’s the easy part, but we don’t really know their distance nor their absolute brightness. If a star looks dim to us, maybe it’s fairly close by but doesn’t emit much energy. Or maybe it is super luminous, but also super far away. It’s hard to distinguish between those cases if stars are only resolved to be points of light.
In everyday life, we have visual clues that are mostly taken for granted:
Those balloons could be in the foreground and tiny, like bugs, but we know the absolute size of them is large, so we know they actually have to be far away in the background.
In practice, then, what we do for some object is
Measure the apparent brightness (how bright it looks)
Somehow find the absolute brightness (the luminosity)
Calculate the distance
For example: Suppose we know (somehow) that Star Alice is exactly as luminous as the Sun, but is measured to be only one trillionth as bright in the sky. But if Alice was at the Sun’s distance it would appear just as bright. How far away would we have to move it so that it goes down by a factor of a trillion in brightness? Well, if brightness goes as the square of the distance,
so then Alice would be
Which is something a little less than 5 pc away. The whole key is finding that luminosity!
Variable Stars!
Wouldn’t it be nice if there were, like, blinking milestones in the Galaxy that told you how far away they are? It turns out that the heavens are very obliging.
Ok, so this isn’t the most dramatic thing, but hopefully if you zoom into the circle you can convince yourself that the highlighted star changed in brightness. These variable stars pulse in a regular pattern because of their mass and stage of evolution — the amazing thing for us is that the rate of pulsation is tightly correlated to its luminosity! And how do we know this? Because we can observe variables close by, where we can find their distance via parallax, and calculate their luminosity. This way we can build a calibrated distance ladder that gets us farther and farther into the Universe. Here, variables like this one are all about 50 times more luminous than the Sun, making it easy to calculate their distance (and then, of course, the distance to the cluster they’re embedded in). There are even brighter classes of variables, called Cepheids, that take us out farther.
To find out how far away very distant galaxies are, we’ll need a new trick…
a trick for another article…
On Deck:
The next article I’m working on is how much energy it would actually take to accelerate even a small mass to close to the speed of light. This seems like a trivial thing in most sci-fi stories, but we’ll see that it’s actually pretty tough.
If you’re a student/teacher and want to see lots of worked examples that I like to include in my classes when I teach the “standard” University Physics 1 and 2 courses, feel free to browse the (growing) collection of 150+ videos at
And if something is especially cool and you’re inclined to leave a “tip” I’m not above coffee or pizza:
Thanks for reading First Excited State! Subscribe for free to receive new posts automatically!





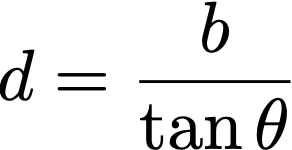







Really clear explanation
Really clear explanation