Pi Day Pi Stuff

(maybe) less familiar relationships between pi and e and the primes!

I snapped awake this morning with klaxons blaring and red alerts flashing — could a science educator/popularizer not write a π-based article on March 14? It is a thing that is apparently compulsory. But do I have anything new to bring to the table aside from reciting the digits or repeating π-based puns that are too embarrassing even for this dad-bod? You, my friends, may be the judge of that in this short e-PI-sode.

BOOM

C’mon, man, that was a good one.

---

The Gaussian Function

I’ve written before about the deep and fascinating connection between the fundamental real numbers (π, e, i, 1, 0) in the sublime Euler’s Equation:

To Be Real

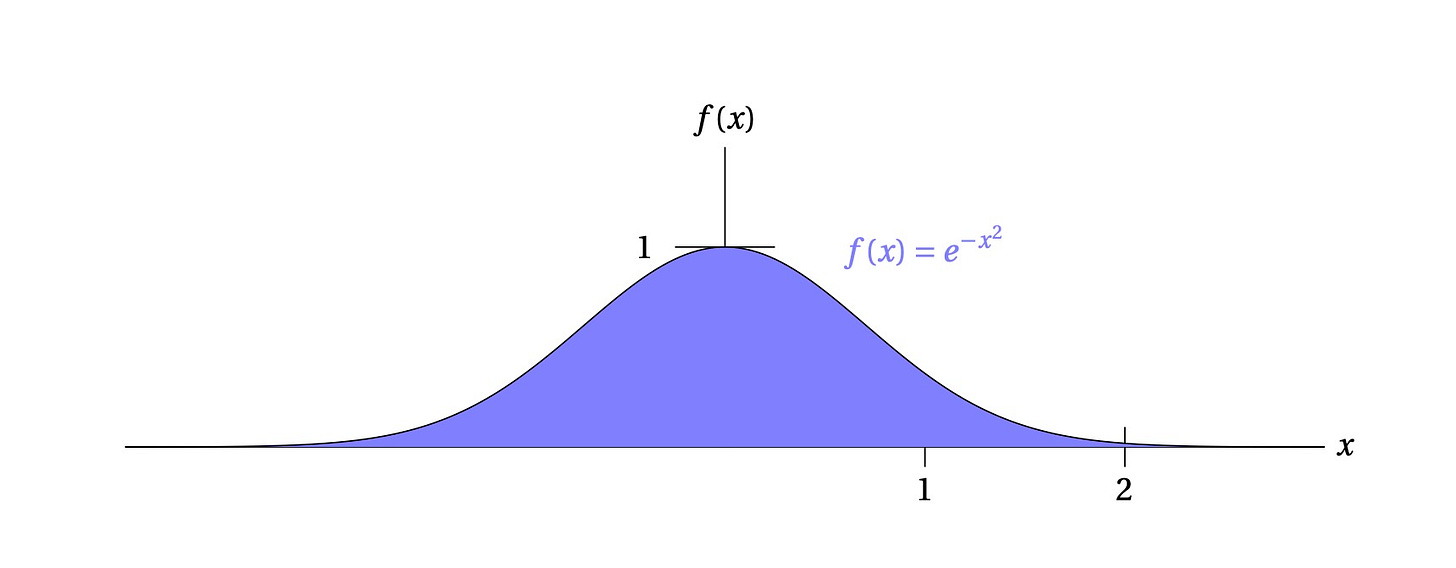
But here’s another one just involving π and e. This is called a Gaussian function in general, and here’s the simplest form:

The connections between this function and usage in mathematics and physics is vast, from quantum mechanics to probability theory. Here I’ll just illustrate a simple and wonderful fact about it:

\(\int_{-\infty}^{+\infty} e^{-x^2} dx = \sqrt{\pi} = 1.77245...\)

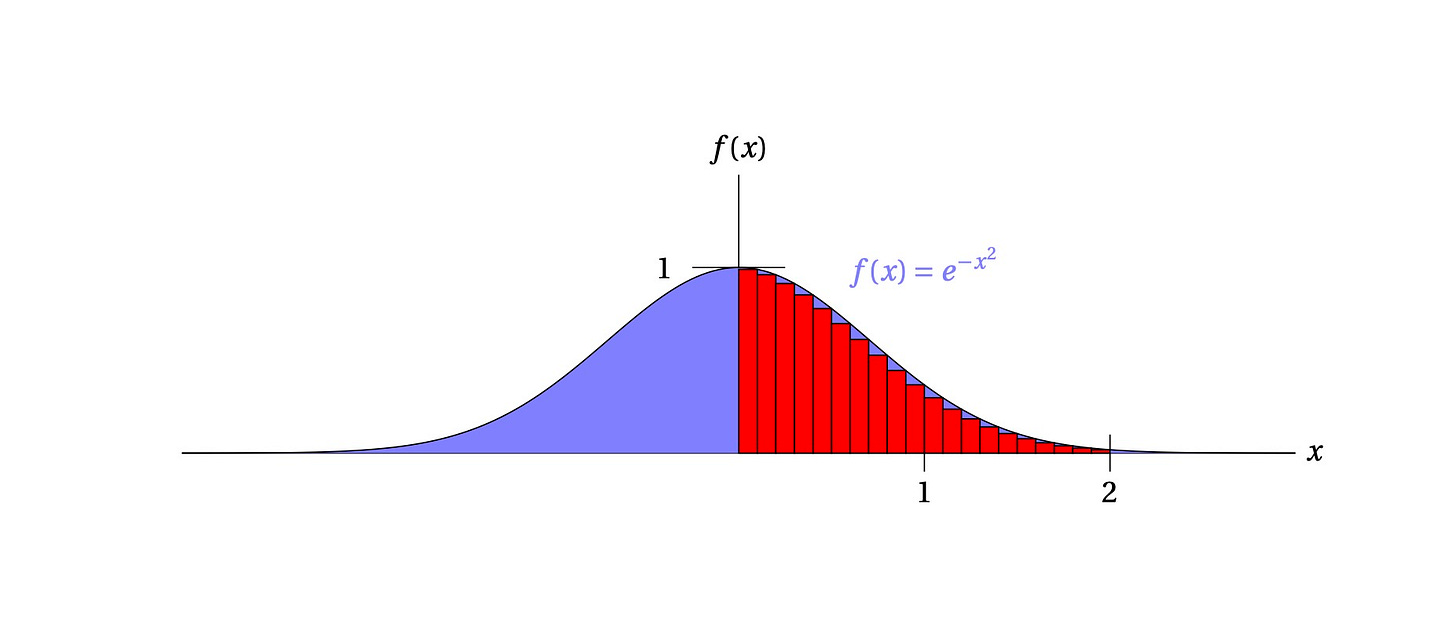
or, in plainer language, the blue region under that curve has an area of the square root of π. Proving that this is so is a standard problem in, say, Calc II, but it’s sort of notoriously difficult for beginning calc students. Let’s check it more simply by just approximating the blue area using a bunch of little rectangles using a spreadsheet (we’re gonna “sheet” this function, as they say on the street). First of all, notice that the blue area looks the same (it’s symmetric) about the vertical line, so we only really have to check some numbers starting with 0 (the right half of the function):

\(\int_{0}^{+\infty} e^{-x^2} dx = \frac{\sqrt{\pi}}{2} = 0.88623...\)

Looking at the image, the total area of the little rectangles is going to be “pretty close” to the blue area, although it looks like the final red sum will be a bit less than the blue total.

You can do this yourself — spreadsheets are marvelous things! I just made the width of each red box 0.1 (in A1) and then the height would be the value of the function at that point (column C). Pulling the formula down to x=2 (and summing up the area of all the boxes) gives:

Yep, a bit under (about 4% off). How could we make it better? Skinnier boxes! Let’s do the same thing, but set the width of each box as 0.01, so we’ll have to drag this out to 200 cells (just the first bit is shown here):

Much closer, as you might suspect. Now we’re only off by about 1%! It’s actually starting to become important that we stopped at x=2 — really, we should carry this out a bit further along the x-axis. You can keep going with thinner and thinner boxes, going on out to x=3 and beyond, and maybe you can convince yourself that you’ll get closer to that exact value of 0.88623… above. I’ll just say that using a programming language like Python is way easier for this kind of thing. Here’s a simple program that makes the boxes 0.000001 wide (so we’re adding up 1 million of them!) and takes the calculation out to x=10:

import math
import sys

dx    = 0.000001
x     = 0
gauss = 0

while (x < 10):
    x = x + dx
    gauss = gauss + math.exp(-(x*x)) * dx

print ("Total: ", gauss)

Now how close are we? Running this program gets us to 0.8862264…, and the exact value is 0.8862269, so we’re less than 1 part in a million away. This, by the way, is actually called (for obvious reasons) numerical integration and is an incredibly powerful tool in scientists’ toolboxes.

It’s not at all obvious to me that there’s a direct connection between the fundamental real number e and π, but there you go. Little connective jewels like this pop up in mathematics from time to time as we explore.

---

π and (all) the Primes

This one might be my favorite. I’m just going to show you the relationship. If your time allows, I really encourage you to just let this thing land and sit in your thoughts for a while. Proving it is a really interesting exercise once you’ve seen the Riemann-Zeta function in school, but that would take us a bit far afield. Here’s a video describing the proof:

Just take a freaking look at this:

That product on the right-hand side involves all the prime numbers. All of them (infinitely many)!!! That there is such a simple relationship between the primes and π is simply astonishing to me. What does it mean? I have no idea. But it’s something I love to think about from time to time.

---

On Deck:

The next article I’m working on is a very basic explanation of what the “metric” in general relativity is all about. If you’ve ever seen the quantity

\(g_{\mu\nu}\)

pop up in more advanced textbooks or articles, that’s what I’m talking about.

---

If you’re a student/teacher and want to see lots of worked examples that I like to include in my classes when I teach the “standard” University Physics 1 and 2 courses, feel free to browse the (growing) collection of 150+ videos at

Physics By Example

And if something is especially cool and you’re inclined to leave a “tip” I’m not above coffee or pizza:

Buy Me a Coffee

---

Thanks for reading First Excited State! Subscribe for free to receive new posts automatically!