Sending a space probe to the outer Solar System is tough. Not only do you have to escape the Earth’s gravity, but you also need enough speed to almost completely climb out of the Sun’s gravitational well; since the Sun is about 300,000 times more massive than the Earth, it’s a tall order. And, the more fuel you pack into a rocket at takeoff, the harder it is to lift off from Earth in the first place.
What would be totally sweet is if there were some way to take off from Earth, go a little ways, and then pick up speed boosts (for free!) as we go along, like mushrooms on a Mario Kart track. Basically, that’s exactly what’s happening when we use the maneuver called the “Gravitational Slingshot” (or “Gravity Assist”, as NASA seems to like to call it).
At first, once you study a little physics, you might wonder how it could possibly work — there’s no doubt that as you approach a massive object (Jupiter, say) your speed will increase, and then if you swing around behind it you’ll indeed be going faster than your initial approach. But as you climb out of Jupiter’s gravitational well, you’ll lose speed, so when you’re far away from it you’ll have the same speed as when you started the encounter. That’s just conservation of energy. So how can we get a net increase? The trick lies in Jupiter’s orbital speed around the Sun.
First, let’s go back and review how we can change reference frames from one observer to another that is in relative motion.
Here’s a simple case of some object being described by “our” frame using the usual vector r — maybe it’s at the coordinates (10, 3) meters. Then at t=0, your friend passes you, moving to the right at a constant 3 m/s. What would be the coordinates of the object for your friend 2 seconds after passing? Well, they’ve moved to the right a distance of 6 meters, so the “primed” coordinates would be (4, 3). In general, then, just using vector math,
And what we’re really interested in are velocities, so then
Ok, let’s see how this works. We’ll assume all these encounters are “elastic”, so no kinetic energy is lost: let’s say a ping-pong ball moves to the right at 10 m/s and collides with a bowling ball moving to the left at 20 m/s.
Using the equations, we’d write
Which reads that the speed of the little ball in the bowling ball’s “rest” frame (in the middle diagram) would be 30 m/s — that should make sense. Now, if the collision is elastic, then in the bowling ball’s frame the little ball just bounces off in the direction it came with the same speed. So switching back out into the “lab” frame, to us it looks like the little ball is traveling at
Very cool. Notice that in the first and third diagram the bowling ball doesn’t change its speed, which makes sense (since it’s far more massive), and the key to this whole idea is to notice that the little ball picks up twice the massive ball’s speed!
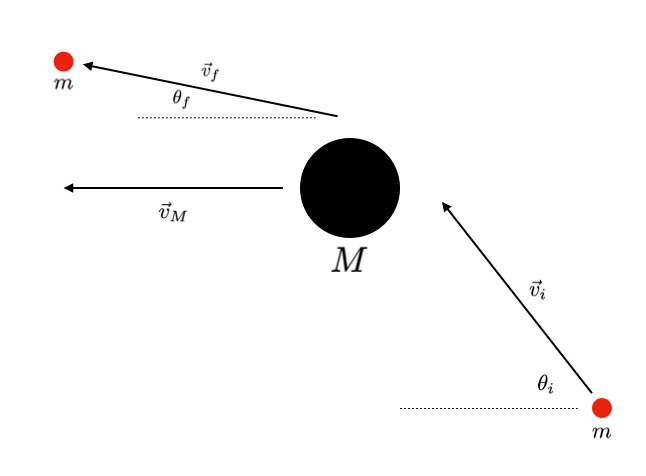
Now we’re ready! Jupiter is far more massive than any spacecraft, so it’ll be our bowling ball, and the spacecraft is the ping-pong ball. And to complicate things, we don’t head straight at Jupiter either, so there are going to be a couple of angles involved. But using the incredibly helpful tools of vector math, it’ll be all right:
Again, this “collision” is elastic, which means that no kinetic energy is lost; if we look at things from Jupiter’s point of view (the primed frame, remember), that means that the spacecraft has the same speed before as it does after:
where the second equation is just what we’d used above. Ok, so now remember that a squared magnitude is just the dot product of a vector with itself, so rewrite the first equation
and substitute the second
Multiply it all out! SO FUN!
Well, Jupiter’s speed cancels from both sides, so that’s nice. But look at the terms involving the final speed of the spacecraft! There’s a squared one, a linear term, and a constant. That’s a quadratic equation!
So, finally, here’s the expression for the final speed of the spacecraft after the encounter in terms of its initial speed, the two angles, and the orbital speed of the planet:
Very cool. Maybe. We’d better check that it gives the right answer for the case we already did above. If the incoming angle is 180 degrees with respect to Jupiter’s motion (opposite!), and the final angle is 0 degrees, then using the speeds we had above (10 and 20) we sure enough get the final speed to be 50. Nice! Let’s put in some “real” data — the first spacecraft to try this maneuver was Pioneer 10 in the early 70s. Before the encounter, the probe had slowed to about 9.5 km/s when it swung by Jupiter, which was orbiting the Sun at about 13.5 km/s. The incoming angle was about 41 degrees and the outgoing was about 7 degrees, so plugging all that in gives a final speed of 22.1 km/s! So Pioneer 10 picked up a “free” 12.6 km/s! In reality, of course, we stole a bit of energy from Jupiter, but it was truly miniscule.
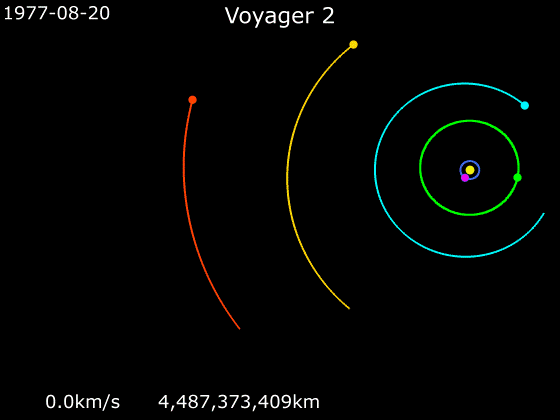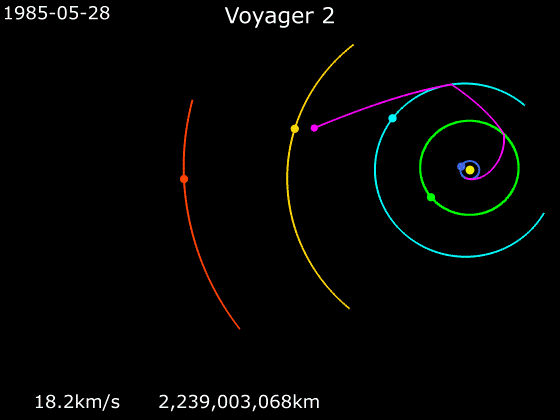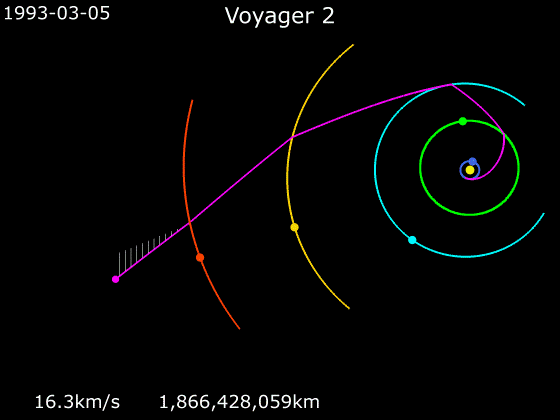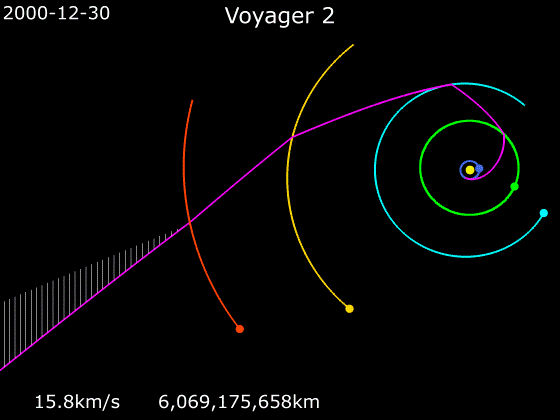
This worked so well that it’s sort of the standard way we send probes to the outer solar system now. Pioneer 11, Voyagers 1 and 2, Galileo, and Cassini (among others) all used this trick. These days, incredibly complex trajectories are undertaken, including slingshots around inner planets like Venus!
Here’s a nice animation of the trajectory of Voyager 2 — it took advantage of the once-in-a-couple-hundred-year alignment of the 4 outer giant planets to do a Grand Tour of the outer solar system with a successive combination of slingshots (that first encounter at Jupiter seems similar to the Pioneer 10 case):
On Deck:
The next article I’m working on is an explanation of why you (or anyone else) can’t go faster than the speed of light. It turns out that it’s not just an engineering question of finding enough thrust, but a limitation of causality itself.
If you’re a student/teacher and want to see lots of worked examples that I like to include in my classes when I teach the “standard” University Physics 1 and 2 courses, feel free to browse the (growing) collection of 150+ videos at
And if something is especially cool and you’re inclined to leave a “tip” I’m not above coffee or pizza:
Thanks for reading First Excited State! Subscribe for free to receive new posts and support my work.





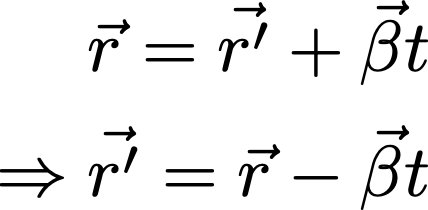





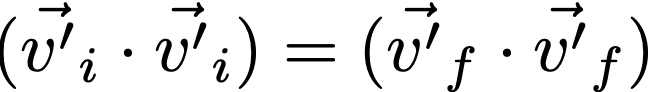





despite being very far from a physicist in my life, one of the first things i wanted to be when i was a kid was a quantum physicist, so this blog is scratching a very good part of my brain