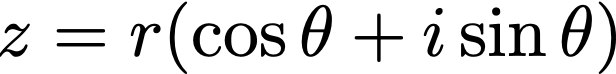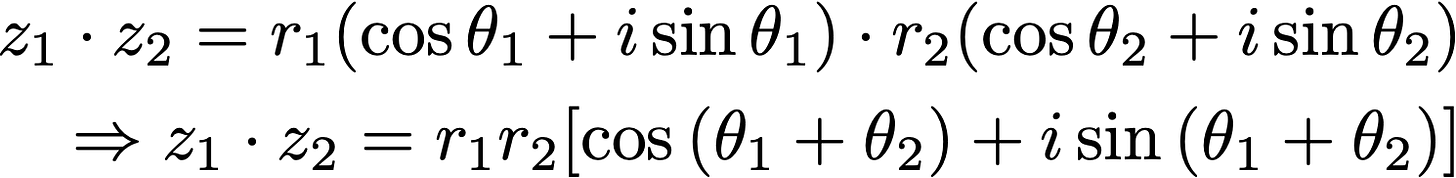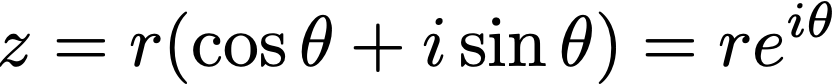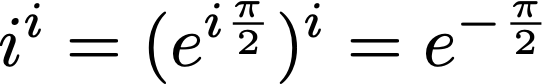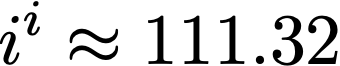Any time you have reason to reference this classic 70’s song, you do it. No questions asked:
Like a good magician, I’m going to tell you exactly what I’m going to do here: I’m going to conjure a real number out of nothing but an “imaginary” number. The common knock against the imaginary number i is that it has no connection to anything “real”, but hopefully we’ll appreciate a bit of a deeper connection by the end.
Look, I’ll even show you what the final trick looks like. It’ll turn out that
See? Nothing but imaginary quantities can generate a real number. It’s a weird-looking construction, though — one immediate objection you might have is what the heck it can possibly mean to raise something to an imaginary power. We’re going to have to build up to that…
What You Find
I suppose, to begin with, the concept of “numbers” is inherently abstract. You could argue that the “real”-ness of a number lies only in its usefulness in mapping to everyday objects. Can you have one apple, or two apples, or some positive integer number of apples? Sure. But you could also have one goat, one nose, one baseball… the things might be real, and the numbers are a useful descriptive mapping onto those things. Then we can imagine situations and predict consequences of “experiments” using these numbers: what would happen if you had 3 apples and I gave you 5 more apples? The numbers (and associated rules) let us predict the final number of apples without actually having to do it.
Now, here’s the problem: we can set up experiments that involve algebraic equations that force us to invent new kinds of numbers. How about this one:
Maybe we’re trying to make a balance sheet of borrowing and lending apples come out right. There’s no positive number of apples that will work, so we’d have to invent the negative integers — they obey the same set of rules, but it’s a further layer of abstraction. Can you have “-2” apples? Not really, but being “owed” 2 apples is a good mapping onto real situations.
Ok, so we can solve many more equations now. But soon maybe we’d encounter one like this:
We’ll have to again extend the idea of a number to include fractions (called the rational numbers). Cool. Are we done?
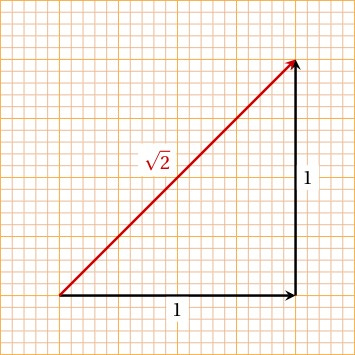
Nope. How about the simple case of finding the length between the corners of a square with each side being 1 unit?
We’d be trying to find the solution of the simple(!) equation
As you might know, there is no integer or fraction that works! The Greek Pythagoras proved this long ago with a brilliant argument — check out
Pythagoras' Proof of Irrational Numbers
The upshot is that this “diagonal number”, the square root of 2, is a number that can’t be represented as a fraction. It’s a never-terminating decimal! So in some crazy sense you really can’t construct an exact diagonal inside a unit square.
This collection of rational (fractions) and irrational numbers are now unified as a dense (“everywhere dense”, amirite math majors?) number line called the real numbers. We need all these numbers to solve, among other things, real-world algebraic problems.
What You Feel
There are still more equations we can’t solve, even with all the real numbers available to us. Here’s the simplest one:
We need some number that, when squared, gives us a negative number. No real number works, so mathematicians bravely invented the number i to fit the bill, assuming that
How many more constructions will there be?? Will we just invent more and more complicated equations that require more elaborate inventions?
NO! We’re done! It turns out you can prove that every algebraic equation can now be solved with these new numbers. Sweet.
Now we just make sure all our rules still apply, so we could multiply i by, say, 4 or add things to it. In fact, we call these complex numbers, and the most general form of them is
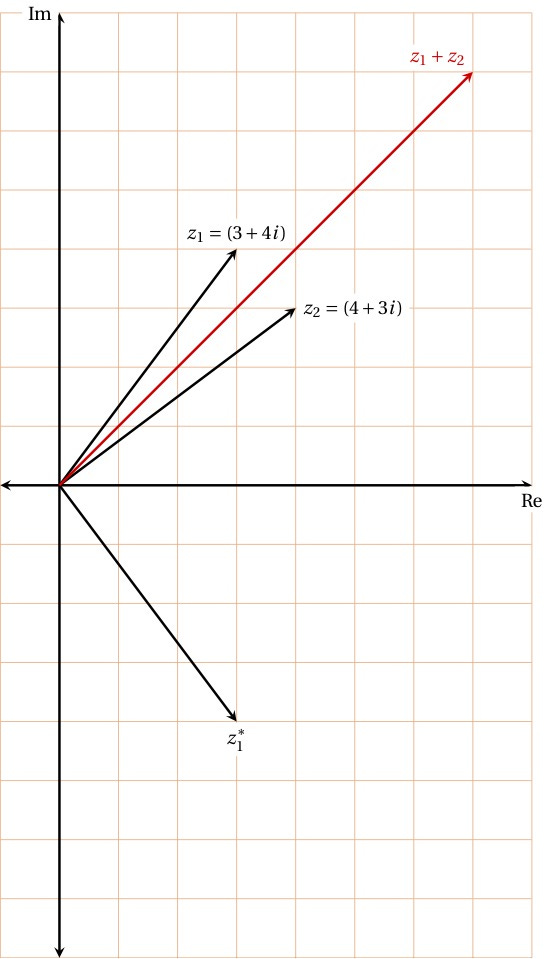
where a and b are real numbers. Complex numbers are typically split into the “a” part (the “real” part) and the “bi” part (the “imaginary” part). When we add complex numbers together, we add the real parts to get a new real part, and the imaginary parts to get a new imaginary part:
This is basically the same operation as adding vectors together, right? So what we do is imagine these complex numbers filling out a 2-D “complex plane” — you learned about the 1-D “number line” most of the way through school, so now you have to expand your mind a bit to imagine two-dimensional numbers! Here’s what that operation looks like, where the real part is on the horizontal axis and the imaginary part is on the vertical:
Can we multiply complex numbers together? Sure, just follow the standard “FOIL” rules:
Is there any intuitive sense in this? At first glance it seems like we’re just getting some arbitrary complex number, but there really is a nifty way to see what happened — we just need to look at this in polar coordinates. Notice we can represent
so then our process of multiplication becomes (algebra!)
where the result follows from a couple of trig identities that no one remembers and everyone has to look up. But look — what’s happening when we multiply complex numbers together is that the “lengths” are multiplied together and then we turn the arrow through the sum of the angles. In our example, the length of each number is 5, and the sum of their angles is 90 degrees, so it makes sense that the product is a vector of length 25 pointing along the vertical (imaginary!) axis! Multiplications, in a complex number space, are basically two operations — scaling and rotating.
I sort of hurried past a subtle thing, though — if we can square i to be -1, then that should work for -i too! The idea is that replacing i → -i shouldn’t change any of our “real” results. This operation of flipping the sign of i is called “complex conjugation” and gets a special little star. You can see that above — what happens when we conjugate a z is that the arrow flips over the real (horizontal) axis. But a cool thing happens if we multiply a number by its complex conjugate:
We get a real number! You always get a real number when you do this. So we’ve made real numbers out of complex ones, but that’s not the whole magic trick yet…
What You Know
I asserted way back up there that we could raise something to an imaginary power. What does that even mean? It sounds ridiculous to multiply, say, 2 by itself i times. But let’s forge ahead anyway: there’s a beautiful way to express raising a number (e, in this case) to some power x by using a result from calculus called Taylor's Theorem:
So, just playing around, let’s replace x by ix and see what happens!
Big deal, you say? It’s a BIG DEAL!!! Of course you immediately recognize(!) that this looks just like the sum of a couple of trigonometric expansions:
with a factor of i missing. I have sort of a lovely vision of cos() and sin() weaved together to form this “complex” tapestry. Putting that in, we get the astonishing relationship
And, for the cherry on top, go ahead and see what happens if you plug in the special value of π for x. Go ahead, see what happens, I’ll wait…
What you got is the most famous equation in mathematics (well-deservedly, I say), Euler’s Equation:
I mean, the more you look at that thing, the more beautiful it gets. 5 of the Universe’s most fundamental constants all related together (e, i, π, 1, 0)! And, amazingly, what do you get if you raise the irrational (never-terminating) number e to the power of another irrational number (pi) multiplied by an imaginary number i? It sounds like you’d get an incomprehensible mess, but you get -1!!! I never tire of looking and thinking about it.
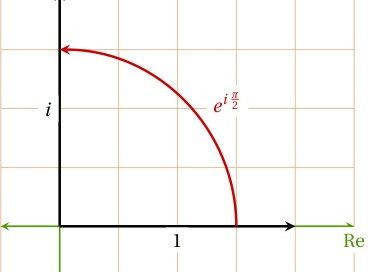
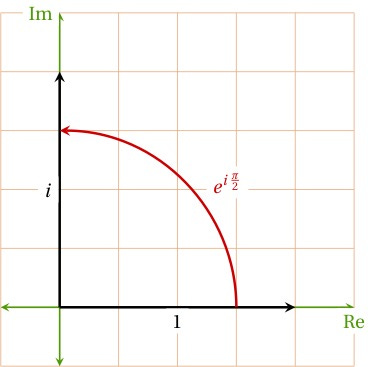
And, just for fun, look what happens if we plug in π/2 instead of π:
Kind of a weird way to write i, but we’ll use this in a minute.
By the way, notice that we can now write complex numbers in a neat and tidy form. This exponential thing looks just like our polar-coordinate representation before! So from now on let’s just write
because now it’s easy to see what happens if we multiply two complex numbers together (no messy algebra or trig identities!)
— multiply the lengths and turn by the sum of the angles!
Now, look at the thing we got above, and just re-write a bit:
Thinking about this geometrically, and remembering that multiplying complex numbers like this basically describes rotations, this is like taking the horizontal unit vector and turning it through the angle π/2 to arrive at a unit vector pointing vertically along the imaginary direction:
To Be Real
Now we’ve finally arrived! You can take the imaginary power of anything!
SO FUN!!!
The final magic trick is, then, to take an imaginary number to an imaginary power. Let’s choose the simplest one, i. And we already had another way to write i:
and you can just plug that into your calculator to find, as promised,
Amazing. A real number pops up out of imaginary things — as close to real magic as we can probably get.
A sort of footnote — I can’t resist pointing out that this is only one of the values. If you think about the geometric construction for a minute, you might point out that, sure, a rotation by π/2 gets you from 1 → i, but so does a rotation by 5π/2, or -3π/2, and so on. It’s a general characteristic when working with complex numbers that solutions tend to be many-valued and periodic. So it’s also true that
if you take the latter of the two rotations.
On Deck:
The next article I’m working on is a dive into finding Lagrange Points — points of stability relative to the Earth’s orbit around the Sun. The inspiration for this is the imminent release of data from the JWST telescope, parked at the special point “L2”.
If you’re a student/teacher and want to see lots of worked examples that I like to include in my classes when I teach the “standard” University Physics 1 and 2 courses, feel free to browse the (growing) collection of 150+ videos at
And if something is especially cool and you’re inclined to leave a “tip” I’m not above coffee or pizza:
Thanks for reading First Excited State! Subscribe for free to receive new posts automatically!